SeGLiR
Javascript library for rapid A/B-testing with Sequential Generalized Likelihood Ratio Tests
Library Reference
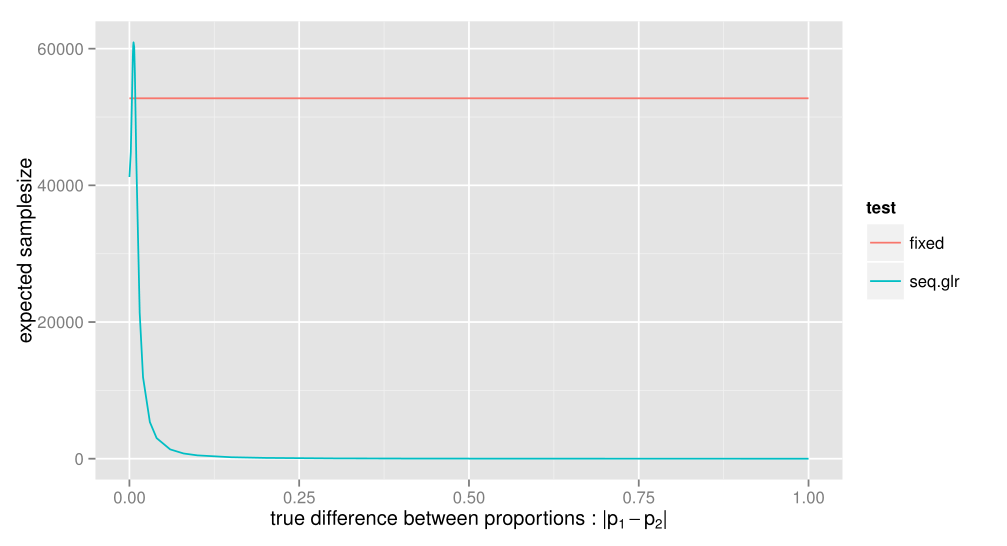
SeGLiR is a javascript implementation of hypothesis testing (aka A/B-testing) with Sequential Generalized Likelihood Ratio Tests (Sequential GLR tests for short). Sequential GLR tests are a family of sequential hypothesis tests that will stop as soon as we are able to reject a hypothesis, while still keeping type-1 and type-2 error guarantees. Compared to fixed-sample size tests, this may give a significant decrease in the needed samplesize, at the cost of a larger worst-case samplesize as well as some loss of precision in estimates when the test is done. The test has been shown1 to be uniformly first-order asymptotically optimal with regard to minimizing samplesize for tests based on a exponential family parameter. To get some idea about the potential savings of the test, here's a comparison of the expected needed samplesize for a fixed samplesize and sequential GLR test in a two-sided comparison of proportions test. Both have $\alpha$-level 0.05, $\beta$-level 0.10 and $\delta$ = 0.01.
Mathematical details
Mathematically, we have one or more random variables $X$ with a distribution dependent on some (possible multivariate) parameter $\theta$. We also have two hypotheses $H_0 : \theta \in \Theta_0$ and $H_A : \theta \in \Theta_A$ and want to decide which is most likely based on data we collect, while keeping some guarantees on how many Type-1 or Type-2 errors we can expect to make. A Sequential GLR test will stop as soon as:
where
and $b_0$ and $b_1$ are thresholds precalculated so that the test fulfills the wanted type-1 and type-2 error guarantees. If $L_{na} > b_0$ at the time of stopping, the null hypothesis is rejected (and the alternative hypothesis accepted), while if $L_{nb} > b_1$ the alternative hypothesis is rejected (and the null hypothesis accepted). Typically there is also a small predefined indifference region of size $\delta$ between $\Theta_0$ and $\Theta_A$ where we don't care about our type-1 and type-2 error guarantees. This is equivalent to saying that we are only interested in detecting differences larger than $\delta$. Note that there is a tradeoff between $\delta$ and worst-case samplesize - reducing $\delta$ will increase the worst-case samplesize, while increasing $\delta$ reduces the worst-case samplesize.
Unlike fixed sample-size tests, the thresholds $b_0$ and $b_1$ for a given $\alpha$-level and $\beta$-level are not analytically calculable, therefore simulation has to be used to calculate these thresholds. Since this can be a time-demanding affair, this library includes some precalculated thresholds for the most common combinations of $\delta$, $\alpha$- and $\beta$-levels. See below for details.
Note that like all sequential tests with a stopping rule, the post-analysis maximum likelihood estimates of the parameter $\theta$ will be biased. Therefore, this library implements the Whitehead method to bias-correct estimates, which can be called with estimate() when the test is done. Confidence intervals are calculated with bias-adjusted bootstrapping, but note that coverage may be poor for some parts of the parameter space, see details below.
Installation and usage
It is easiest to install SeGLiR via node package manager (make sure you have node.js installed):
npm install seglir
and load via require in node.js.
var glr = require('seglir');
Generally the library follows the template of creating an instance of a test via :
var test = glr.test(type, sides, indifference_size, alpha, beta);
where type is the type of the test (for instance "bernoulli"), sides is "two-sided" or "one-sided", indifference_size is the size of the indifference region, alpha is the desired type-1 error, and beta is the desired type-2 error. These parameters may vary depending on the type of test, so check documentation for the test type below. Note that in a lot of cases, calculating the thresholds $b_0$ and $b_1$ in order to get the wanted $\alpha$- and $\beta$-level may take a long time, so it's an advantage to select alpha and beta values where the thresholds are precalculated, see this under the specific test. If the precalculated thresholds are not available for the wanted combination of $\delta$, $\alpha$- and $\beta$-level, SeGLiR will try to calculate these thresholds by simulation when instantiating the test. If the simulation fails to converge, it might be necessary to find the thresholds manually with the functions alpha_level() and beta_level().
From the returned instance of the test, you can add samples via the function addData():
test.addData({x : 0});
test.addData({x : 1, y : 0});
test.addData({y : 0});
test.estimate();
This library currently implements these types of Sequential GLR tests:
- Comparing two bernoulli proportions
- Comparing two gaussian means, with equal and either known or unknown variance
- Selecting the best arm in a two-armed bandit setting, with δ-PAC guarantees
There are some differences between the functions for these tests, so consult more detailed reference for each test below.
Comparison of two bernoulli proportions
In these tests we assume that we have two random variables, $X$ and $Y$, where $X$ is bernoulli distributed with unknown parameter $p_1$ and $Y$ is bernoulli distributed with unknown parameter $p_2$, and we want to detect whether there is a difference between $p_1$ and $p_2$. These tests are what is commonly used in web page testing, for instance for comparing conversion rates.
In the two-sided test we test the hypotheses $H_0 : p_1 = p_2$ versus $H_A : |p_1 - p_2| > \delta$ (where $\delta > 0$ is the size of the indifference region), while in the one-sided test we test the hypotheses $H_0 : p_1 - p_2 < - \delta$ versus $H_A : p_1 - p_2 > \delta$. Note that in both cases, this is equivalent to saying we are interested in detecting differences between $p_1$ and $p_2$ larger than $\delta$.
Test instantiation:
- seglir.test("bernoulli", sides, indifference, alpha, beta, simulateThreshold)
- sides : "one-sided" or "two-sided"
- indifference : the value of $\delta$, i.e. the size of the indifference region
- alpha : the wanted level of type-1 errors
- beta : the wanted level of type-2 errors
- simulateThreshold : whether to calculate thresholds by simulation. When manually calculating thresholds, this can be set to false.
Instance functions
- getResults() : returns an object with sufficient statistics, likelihood ratio statistics, as well as information on whether the test is done.
- pValue() : if the test is done, this will simulate the p-value.
- confInterval() : if the test is done, this returns a bootstrap confidence interval of the difference between $p_1$ and $p_2$.
- estimate(max_samples, bias_correct) : if the test is done, this returns whitehead bias-adjusted estimates of $p_1$, $p_2$ and $p_1 - p_2$ respectively. max_samples is an optional parameter for setting max number of simulations used in estimation. Whitehead bias-correction can be disabled by setting optional parameter bias_correct to false.
- getData() : returns two arrays with the sequences of samples of $X$ and $Y$ collected so far.
- addData({x : 1, y : 1}) : add data points from samples of $X$ and $Y$ respectively. Note that it's possible to add samples from $X$ and $Y$ separately. Returns undefined until test is finished, when it will return either "true" ($H_A$ was rejected) or "false" ($H_0$ was rejected) as a string. Note that after the test is finished, the instance will still store new samples added, but test statistics and conclusion will not be updated. All stored samples collected can be retrieved via getData().
- expectedSamplesize(p1, p2) : simulates the expected sample size needed for concluding a test with true parameters $p_1$ and $p_2$.
- maxSamplesize() : returns the worst-case maximum samplesize of this test.
- properties : returns an object with properties of this test that were specified on initialization, such as type, sides, indifference size, alpha and beta.
- alpha_level(b0, b1, samples) : simulate the alpha level for the given thresholds $b_0$ and $b_1$. Returns the mean and bootstrapped standard error of the simulated alpha level.
- beta_level(b0, b1, samples) : simulate the beta level for the given thresholds $b_0$ and $b_1$. Returns the mean and bootstrapped standard error of the simulated alpha level.
Precalculated thresholds:
- Two-sided: $\alpha$-level 0.05, $\beta$-level 0.10, 0.20, indifference region of size 0.2, 0.1, 0.05, 0.025, 0.01.
- One-sided: $\alpha$-level 0.05, $\beta$-level 0.05, 0.10, indifference region of size 0.2, 0.1, 0.05, 0.025, 0.01.
A simple example:
var glr = require('seglir');
var test = glr.test("bernoulli","two-sided",0.01,0.05,0.10);
// add data from samples as they come in
test.addData({x : 0});
test.addData({y : 1});
test.addData({y : 1, x : 0});
test.addData({x : 0, y : 1});
test.addData({y : 1, x : 0}); // returns result "false", i.e. we reject the null-hypothesis
// get estimates of p_1, p_2 and p_1-p_2
test.estimate(); // returns [0, 1, -1]
Comparison of two normal means
In these tests we assume that we have two normal random variables, $X$ and $Y$, with $X \sim N(\mu_1,\sigma^2)$ and $Y \sim N(\mu_2,\sigma^2)$, where $\mu_1$ and $\mu_2$ is unknown, $\sigma^2$ may be known or unknown, and we want to detect differences between $\mu_1$ and $\mu_2$.
In the two-sided test we test the hypotheses $H_0 : \mu_1 = \mu_2$ versus $H_A : |\mu_1 - \mu_2| > \delta$ (where $\delta > 0$ is the size of the indifference region), while in the one-sided test we test the hypotheses $H_0 : \mu_1 - \mu_2 < - \delta$ versus $H_A : \mu_1 - \mu_2 > \delta$. Note that in both cases, this is equivalent to saying we are interested in detecting differences between $\mu_1$ and $\mu_2$ larger than $\delta$.
Note that in the case that the variance $\sigma^2$ is unknown, we need to specify some upper bound on the variance in order to be able to give type-1 and type-2 error guarantees. It is therefore needed to at least have some ballpark estimate of the variance before using this test.
Test instantiation:
- seglir.test("normal", sides, indifference, alpha, beta, variance, variance_bound, simulateThreshold)
- sides : "one-sided" or "two-sided"
- indifference : the value of $\delta$, i.e. the size of the indifference region
- alpha : the wanted level of type-1 errors
- beta : the wanted level of type-2 errors
- variance : the variance of X and Y, if it is known, undefined otherwise.
- variance_bound : if variance is undefined, i.e. the variance is unknown, some upper bound on the variance must be specified.
- simulateThreshold : whether to calculate thresholds by simulation. When manually calculating thresholds, this can be set to false.
Instance functions
- getResults() : returns an object with sufficient statistics, likelihood ratio statistics, as well as information on whether the test is done.
- pValue() : if the test is done, this simulates the p-value.
- confInterval() : if the test is done, this returns a bootstrap confidence interval of the difference between $\mu_1$ and $\mu_2$.
- estimate(max_samples, bias_correct) : if the test is done, this returns whitehead bias-adjusted estimates of $\mu_1$, $\mu_2$ and $\mu_1 - \mu_2$ respectively. max_samples is an optional parameter for setting max number of simulations used in estimation. Whitehead bias-correction can be disabled by setting optional parameter bias_correct to false.
- getData() : returns two arrays with the sequences of samples of $X$ and $Y$ collected so far.
- addData({x : 9.2, y : 8.5}) : add data points from samples of $X$ and $Y$ respectively. Note that it's possible to add samples from $X$ and $Y$ separately. Returns undefined until test is finished, when it will return either "true" ($H_A$ was rejected) or "false" ($H_0$ was rejected) as a string. Note that after the test is finished, the instance will still store new data points added internally, but test statistics and conclusion will not be updated. All stored data points collected can be retrieved via getData().
- expectedSamplesize([mu1,variance], [mu2,variance]) : simulates the expected sample size needed for concluding a test with true means $\mu_1$, $\mu_2$ and variance as given.
- properties : returns an object with properties of this test that were specified on initialization, i.e. type, sides, indifference size, alpha, beta, variance and variance_bound.
- alpha_level(b0, b1, samples) : simulate the alpha level for the given thresholds $b_0$ and $b_1$. Returns the mean and bootstrapped standard error of the simulated alpha level.
- beta_level(b0, b1, samples) : simulate the beta level for the given thresholds $b_0$ and $b_1$. Returns the mean and bootstrapped standard error of the simulated alpha level.
Precalculated thresholds:
- Two-sided: $\alpha$-level 0.05, $\beta$-level 0.10, indifference region of size 0.1, 0.05, 0.025, 0.01, at either variance 1 or variance-bound 1.
- One-sided: $\alpha$-level 0.05, $\beta$-level 0.05, indifference region of size 0.1, 0.05, 0.025, 0.01, at either variance 1 or variance-bound 1.
A simple example:
var glr = require('seglir');
var test = glr.test("normal","two-sided",0.1,0.05,0.1,1)
// add data from samples as they come in
test.addData({'x':5.2})
test.addData({'y':8.3})
test.addData({'x': 4.7, 'y': 7.1})
test.addData({'x': 2.0, 'y' : 9.0}) // returns 'false', i.e. we reject the null-hypothesis
// get estimates of mu_1, mu_2 and mu_1-mu_2
test.estimate() // returns [4.1673, 7.9274, -3.7601]
Best arm selection with δ-PAC guarantees
These are a slightly different type of tests than those above. We assume we have two "arms", a la a multi-armed bandit problem, and want to find out which "arm" is the best with regard to some parameter. We also want to have some guarantee on how likely we are to actually select the best arm, called a δ-PAC guarantee, so that the probability of the correct choice is at least $1 - \delta$. This can be viewed as a multi-armed bandit problem with a "pure-exploration" (as opposed to "exploration-exploitation") strategy. Sequential GLR tests have been shown2 to be optimal with regard to samplesize for these type of problems. For more details, see Emilie Kaufmann's PhD thesis.
Note that these tests are similar to a regular two-sided Sequential GLR test with $\delta = 0$. Since there is no indifference region (i.e. we are interested in detecting a difference, no matter how small) there is no worst-case samplesize for these tests, which may lead to the test taking a very long time if the "arms" are close to equally as good.
Best arm selection with bernoulli arms
In these tests we assume that we have two random variables, $X$ and $Y$, where $X$ is bernoulli distributed with unknown parameter $p_1$ and $Y$ is bernoulli distributed with unknown parameter $p_2$, and we want to find which variable has the highest value of $p$.
Test instantiation:
- seglir.test("bernoulli_pac", delta)
- delta : the wanted error guarantee
Instance functions
- getResults() : returns an object with sufficient statistics, likelihood ratio statistics, as well as information on whether the test is done.
- confInterval() : if the test is done, this returns a bootstrap confidence interval of the difference between $p_1$ and $p_2$.
- estimate(max_samples, bias_correct) : if the test is done, this returns whitehead bias-adjusted estimates of $p_1$, $p_2$ and $p_1 - p_2$ respectively. max_samples is an optional parameter for setting max number of simulations used in estimation. Whitehead bias-correction can be disabled by setting optional parameter bias_correct to false.
- getData() : returns two arrays with the sequences of samples of $X$ and $Y$ collected so far.
- addData({x : 1, y : 1}) : add data points from samples of $X$ and $Y$ respectively. Note that it's possible to add samples from $X$ and $Y$ separately. Returns undefined until test is finished, when it will return either "X" (i.e. $p_1 > p_2$) or "Y" ($p_2 > p_1$) as a string. Note that after the test is finished, the instance will still store new sampels added, but test statistics and conclusion will not be updated. All stored samples collected can be retrieved via getData().
- expectedSamplesize(p1, p2) : simulates the expected sample size needed for concluding a test with true parameters $p_1$ and $p_2$.
- properties : returns an object with properties of this test that were specified on initialization, i.e. delta.
A simple example:
var glr = require('seglir');
var test = glr.test("bernoulli_pac", 0.05);
// add data from samples as they come in
test.addData({x : 0});
test.addData({y : 1});
test.addData({y : 1, x : 0});
test.addData({x : 0, y : 1}); // returns result "Y", i.e. p_1 > p_2
// get estimates of p_1, p_2 and p_1-p_2
test.estimate(); // returns [0, 1, -1]
Best arm selection with normal arms
In these tests we assume that we have two random variables, $X \sim N(\mu_1,\sigma^2)$ and $Y \sim N(\mu_2,\sigma^2)$, where $\mu_1$, $\mu_2$ is unknown, $\sigma^2$ is known, and we want to detect which variable has the highest mean $\mu$.
Test instantiation:
- seglir.test("normal_pac", delta, variance)
- delta : the wanted error guarantee
- variance : the known variance
Instance functions
- getResults() : returns an object with sufficient statistics, likelihood ratio statistics, as well as information on whether the test is done.
- confInterval() : if the test is done, this returns a bootstrap confidence interval of the difference between $\mu_1$ and $\mu_2$.
- estimate(max_samples, bias_correct) : if the test is done, this returns whitehead bias-adjusted estimates of $\mu_1$, $\mu_2$ and $\mu_1 - \mu_2$ respectively. max_samples is an optional parameter for setting max number of simulations used in estimation. Whitehead bias-correction can be disabled by setting optional parameter bias_correct to false.
- getData() : returns two arrays with the sequences of samples of $X$ and $Y$ collected so far.
- addData({x : 2.3, y : 9.8}) : add data points from samples of $X$ and $Y$ respectively. Note that it's possible to add samples from $X$ and $Y$ separately. Returns undefined until test is finished, when it will return either "X" (i.e. $\mu_1 > \mu_2$) or "Y" ($\mu_2 > \mu_1$) as a string. Note that after the test is finished, the instance will still store new data points added internally, but test statistics and conclusion will not be updated. All stored data points collected can be retrieved via getData().
- expectedSamplesize([mu_1,variance], [mu_2,variance]) : simulates the expected sample size needed for concluding a test with true means $\mu_1$, $\mu_2$ and variance as given.
- properties : returns an object with properties of this test that were specified on initialization, in this case delta.
A simple example:
var glr = require('seglir');
var test = glr.test("normal_pac",0.05,1)
// add data from samples as they come in
test.addData({'x':5.2})
test.addData({'y':8.3})
test.addData({'x': 4.7, 'y': 7.1})
test.addData({'x': 2.0, 'y' : 9.0}) // returns 'Y', i.e. mu_2 > mu_1
// get estimates of mu_1, mu_2 and mu_1-mu_2
test.estimate() // returns [4.0177, 8.0822, -4.0617]
1. Tartakovsky, Nikiforov, Basseville : Sequential Analysis, CRC press 2014, Theorem 5.4.1
2. E. Kaufmann, O. Cappé, A. Garivier : On the Complexity of Best Arm Identification in Multi-Armed Bandit Models, arXiv 2014